Science
The latest in science news, from the depths of space to the quantum realm.
Camera captures the world as animals see it, with up to 99% accuracy
January 25, 2024
It’s easy to forget that most animals don’t see the world the way humans do. In fact, many perceive colors that are invisible to us. But now, for the first time, scientists have found a way to capture footage as seen by animals, and it's mesmerizing.
Energy
-
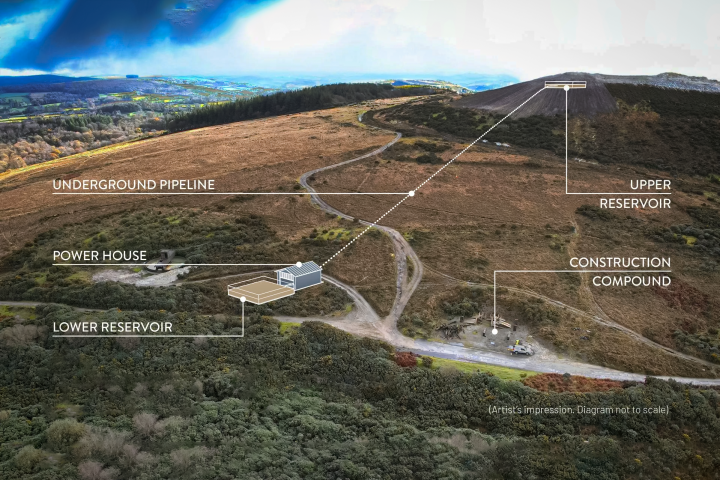
Advanced 'high-density waterless hydro' energy plant gets green light
May 01, 2024This remarkable project promises to open up zero-carbon energy storage to a broad range of areas without huge hills, delivering 2.5 times the power of water-based hydro. A pilot plant has been greenlit, with full-size, grid-scale projects to follow. -
World first energy storage unit demonstrates zero degradation over 5 years
April 15, 2024China's CATL – the world's largest EV battery producer – has launched TENER, which is described as the "world's first mass-producible energy storage system with zero degradation in the first five years of use." -
90-GWh thermal energy storage facility could heat a city for a year
April 09, 2024An energy supplier in Finland has announced the upcoming construction of an underground seasonal thermal energy storage facility about the size of two Madison Square Gardens that could meet the heating demands of a medium-sized city for up to a year.
Load More
Medical
-
Experimental antibody drug prevents and even reverses diabetes onset
May 01, 2024A promising new drug could prevent and even reverse the onset of type 1 diabetes. The experimental monoclonal antibody drug was found to act like a shield to protect insulin-producing cells from damage and even extended lifespan in some cases. -
Only half of atrial fibrillation patients survive 10 years after treatment
April 30, 2024Examining long-term outcomes for people with atrial fibrillation, the most common heart rhythm disorder, a new study found that 55% survived to 10 years. The researchers say it needs to be treated as a chronic illness with serious long-term consequences. -
Bacterial enzyme strips away blood types to create universal donor blood
April 29, 2024Using enzymes produced by a bacteria that almost everyone has in their gut, researchers have removed the antigens from red blood cells that determine blood type, putting us within reach of producing universal donor blood.
Load More
Space
-
Boeing's crewed Starliner launches Monday. Here's why it's a big deal
April 29, 2024The embattled Boeing spacecraft Starliner is scheduled to launch next week, after more than a decade of delays and development. Given the history of the craft and the company's recent scandals, it's a nail-biter – so let's recap CST-100 Starliner. -
Nearby asteroid's birthplace traced to specific crater on the Moon
April 26, 2024Many asteroids can be traced back to their parent body – the planet or moon they broke off from. But for the first time, scientists now claim to have traced the origins of an asteroid back to the specific crater it was birthed from. -
NASA just hacked a 1977 computer on a spacecraft way out past Pluto
April 23, 2024We have to cut the 47-year-old space veteran some slack – it's faring much better than our 2019 laptops – but Voyager 1's five months of communicating nonsense to Earth may be over, thanks to Mission Control's 15-billion-mile remote IT fix.
Load More
Materials
-
Almost 100%-recyclable circuit board turns to jelly for disassembly
April 29, 2024A new type of printed circuit board could drastically reduce the amount of electronic waste that ends up in landfills. Although most PCBs are difficult to recycle, such is not the case with this one, which turns into a reusable jelly when necessary. -
Goldene: New 2D form of gold makes graphene look boring
April 16, 2024Graphene is the Novak Djokovic of materials – it’s so damn talented that it’s getting boring celebrating each new victory. But an exciting new upstart is challenging graphene’s title. Meet goldene, a 2D sheet of gold with its own strange properties. -
Graphite platform levitates without power
April 10, 2024Magnetic levitation is used to float things like lamps and trains, but usually it requires a power source. Now, scientists in Japan have developed a way to make a floating platform that requires no external power, out of regular old graphite.
Load More
Biology
-
T. Rex was not as smart as we were made to believe
April 30, 2024While we don't like to talk ill of the dead, new analysis has called into question the intelligence of the king of the dinosaurs. It upends last year's findings that likened the cognitive skills of the Tyrannosaurus rex to that of a primate. -
Giant raptor dinosaur had legs taller than you
April 29, 2024The six-foot-tall raptors in the Jurassic Park movies were terrifying enough, but now scientists have described a giant new raptor species whose legs alone were that tall. -
Monstrous prehistoric salmon had "tusks like a warthog"
April 25, 2024If a giant prehistoric salmon isn't scary enough for you, how about one with warthog-like tusks? According to a new study, Oncorhynchus rastrosus possessed just such appendages – even though the fish likely fed on tiny plankton.
Load More
Environment
-
Plastic embedded with plastic-eating spores is degradable – and tougher
April 30, 2024A new biodegradable plastic embedded with spores of plastic-eating bacteria manages to break down 90% of the material after five months in landfill. Weirdly, this actually made the plastic tougher and stronger during use. -
Soybean waste used to grow good "green" food for farmed fish
April 26, 2024Fish farming may be getting much more eco-friendly, courtesy of soybean processing wastewater. Microbes in the liquid have been used to produce proteins that could replace the fishmeal which is currently fed to farmed fish. -
Superfood protein pulled out of thin air massively scales up production
April 24, 2024It's super-sustainable, easily made and nutrient-dense. And it puts all other food production to shame. Now, the first air-protein factory is open. It's the food of the future, and soon a $100 million industry – but will you be putting it on your plate?
Load More
Physics
-
Think you understand evaporation? Think again, says MIT
April 25, 2024We all know that water evaporates when the temperature climbs, but researchers have just shown that there's another factor at play. The breakthrough could solve long-standing atmospheric mysteries and lead to future technological advances. -
Free software lets you design and test warp drives with real physics
April 16, 2024Warp drives are among the more plausible of science fiction concepts, at least from a physics perspective. Now, a group of scientists and engineers has launched open-source software that lets you design and test scientifically accurate warp drives. -
Professor Peter Higgs, renowned for Higgs boson prediction, dies aged 94
April 09, 2024Professor Peter Higgs has died aged 94. The theoretical physicist was best known for his prediction of a key elementary particle, the Higgs boson, which earned him the 2013 Nobel Prize in Physics soon after its discovery.
Load More
Electronics
-
AI synthesizer bridges technology and creativity in music composition
February 15, 2024SPIN challenges conventional notions of music creation by inviting users to collaborate with an AI language model called MusicGen. With its distinctive blend of a turntable and a drum machine, SPIN offers users a creative music composition tool. -
Eye-tracking window tech tells sightseers about what they're looking at
January 05, 2024If you're on a sightseeing tour in a bus, you really don't want to be looking away from the passing attractions to Google them on your smartphone. The AR Interactive Vehicle Display is intended to help, by showing relevant information on the vehicle's window glass. -
Diamond data storage breakthrough writes and rewrites down to single atom
December 05, 2023Diamond is a promising material for data storage, and now scientists have demonstrated a new way to cram more data onto it, down to a single atom. The technique bypasses a physical limit by writing data to the same spots in different-colored light.
Load More
Quantum Computing
-
Diamond-stretching technique makes qubits more stable and controllable
November 30, 2023Researchers are claiming a breakthrough in quantum communications, thanks to a new diamond-stretching technique they say greatly increases the temperatures at which qubits remain entangled, while also making them microwave-controllable. -
Perovskite LED unlocks next-level quantum random number generation
September 05, 2023Random numbers are critical to encryption algorithms, but they're nigh-on impossible for computers to generate. Now, Swedish researchers say they've created a new, super-secure quantum random number generator using cheap perovskite LEDs. -
Silicon quantum computing surpasses 99% accuracy in three studies
January 19, 2022Three teams of scientists have achieved a major milestone in quantum computing. All three groups demonstrated better than 99 percent accuracy in silicon-based quantum devices, paving the way for practical, scalable, error-free quantum computers.
Load More