An invitation-only conference held back in 2011 on the topic "Quantum Physics and the Nature of Reality" (QPNR) saw top physicists, mathematicians, and philosophers of science specializing in the meaning and interpretation of quantum mechanics wrangling over an array of fundamental issues. An interesting aspect of the gathering was that when informally polled on the main issues and open problems in the foundations of quantum mechanics, the results showed that the scientific community still has no clear consensus concerning the basic nature of quantum physics.
Quantum mechanics (QM), together with its extensions into quantum electrodynamics and quantum field theory, is our most successful scientific theory, with many results agreeing to better than a part in a billion with experiment. However, at its roots QM is ghost-like – when you try to pin down just what it means, it tends to slip between the fingers. It is full of apparent paradoxes, incompatible dualities, and "spooky actions." Simply put, although QM works amazingly well, why and how it works remains elusive.
While it's unlikely that many physicists lose much sleep over the meaning of quantum mechanics, the advent of quantum information physics (quantum cryptography, quantum computing, etc.) has directly confronted them with many fundamental questions about QM. Quantum mechanics works regardless of interpretation, but our intuition seems to be very weak when applied to situations that bring out the stranger aspects of QM. As a result, the amount of effort applied to clarifying the foundations of QM has increased considerably over the past three decades.
What, then, does the QPNR poll tell us about the state of our knowledge of quantum mechanics? While it is impractical to poke into every nook and cranny of the poll, the answers to a few of the questions merit our attention. (Note that people were allowed to vote for more than one answer, so the percentages in the source sometimes do not add up to 100 percent. I have taken the liberty of normalizing the results so they do equal 100 percent, and in some cases I have simplified the issues to more clearly state the options.)
Introduction to QM
We'll start with a QPNR poll question about the quantum measurement problem, as this will provide the opportunity to introduce some of the main concepts in QM. In QM, the wavefunction of an object describes all measurable properties of that object. It is a complete description of what is called the quantum state of that object. The wavefunction is governed by the Schrödinger equation, which tells the wavefunction how to change in response to external conditions.
The mathematical details are not important right now, save for one – the Schrödinger equation is a linear equation. If you add together several different solutions to a linear equation, that sum is also a solution. This is called the principle of superposition, and is not a physical result, but rather a property of the basic mathematical structure of QM. The implication is that there exist a class of wavefunctions, called quantum superpositions, which simultaneously describe multiple quantum states of an object.
Let's put an object into a superposition, measure it, and see what results are found according to standard quantum mechanics. Begin with a red QM ball and a green QM ball that are otherwise identical. Set them each rotating with two quanta (one quantum is considered half a unit) of angular momentum (which we will call spin) so that the red ball has its spin up, while the blue ball has its spin down. The quantum state of the two balls before they interact is red-up + blue-down. If you measure the spin of the two balls, you will find the red ball always has a spin of +1, and the blue ball always has a spin of -1, making the total spin of the pair equal to zero. This is important because the total spin of a system is constant in QM.
Now knock the balls together. If their surfaces have some property analogous to friction, the two balls can pass spin from one to the other. The most likely results are no change (red-up + blue-down, which we'll call [1 -1]); spin exchange (red-down + blue-up, or [-1 1]); and spin cancellation (red-0 + blue-0, or [0 0]). As any of the three can happen, before either of the balls are measured they are in a state of entangled superposition. Their quantum state after colliding and before measuring is [1 -1] + [-1 1] + [0 0].
[For the quantum skeptics: If we measure the spin of the red and blue balls along different directions, Bell's theorem tells us that the correlations between the measurement results will be stronger than is possible for classical or predetermined systems. This theoretical result is also what is observed experimentally, providing experimental evidence that the spins of the balls following the collision have no definite value until they are measured.]
After the collision, measure the spin of the red ball. If you measure a spin of 1, the quantum state of the two balls after the measurement is the [1 -1] state – the other two superposed states have vanished, as they are not consistent with the measurement. Similarly, if the measurement is -1 or zero, after those measurements the quantum state of the two balls is [-1 1] and [0 0], respectively. Any states inconsistent with the measurement result disappear, even though those states existed in the original superposition.
The quantum measurement problem
So what happens if we decide to really believe quantum mechanics? Quantum mechanics is supposed to describe all measurable phenomena, after all. The instrument that measures spin is a rather complex quantum system, and the person operating it is a more complex quantum system. If I can get three different results out of a spin measurement, why don't I go into a superposition of having measured each of the three possible results?As far as we know, no human has ever noticed being in a superposed state – even though we don't really know what that would feel like. The result of a measurement such as that described above is, in our experience, a single definite number.
To make QM treat observers as our experience suggests, standard QM assumes that measuring devices and observers are classical in their behavior. No superpositions of classical measuring devices and observers can exist, so measurements give a single unambiguous answer, just as we expect. This was originally thought to be a reasonable assumption, but has caused many arguments and sleepless nights among quantum physicists.
The problem is that there is every reason to believe that measuring devices and observers are not truly classical in behavior. Rather, their QM wavefunction combined with the Schrödinger equation provides a complete description of the possible behaviors of the object.
The nonclassical behavior of large measuring devices has been proven within standard QM by the insolubility theorem. If the structure of QM does hold for all systems, then at the end of a measurement process the observer, the measuring apparatus, and the object being measured exist in a quantum superposition of all states consistent with the wavefunction of the object being measured.
Given this, the quantum measurement problem can be summarized thusly: Why do measurements taken by complex, large-scale quantum devices (including ourselves) appear to have a single, definite result? If some aspect of QM interactions does cause the measurement process to narrow to a specific result, what is it? Does it exist within properties of quantum systems having many degrees of freedom, or does QM need to be extended?
- The original notions of collapsing wavefunctions and classical observers were an attempt to answer this question, but the insolubility theorem shows this is inadequate for the purpose.
- Some have proposed that the Schrödinger equation should be altered to include some nonlinear terms that will produce pure states under measurement. These attempts have their own problems, primarily because standard quantum mechanics works so well – it is difficult to change its fundamental equation without spoiling the good parts.
- In Everett-type many-worlds theories, carrying out a measurement with multiple results causes the formation of a set of alternate universes – one for each possible result. This avoids the measurement problem – the observer splits with the measuring device, and so doesn't notice the multiplicity. But you have to be able to believe that bouncing a photon off an atom creates new universes...
- Decoherence, which results from the interaction of a quantum system with its surroundings, can render the superposed states of the wavefunction incapable of interfering with each other, at which point their probabilities become independent. Some believe this takes the place of wavefunction collapse, but others believe it has no bearing at all on the measurement problem, as all that is accomplished is to make a superposition with the entangled environment.
So what did the QPNR poll say about the quantum measurement problem?
- Pseudoproblem (will go away with additional work) – 20%
- Solution through decoherence – 11%
- Solution in some other manner – 30%
- Seriously threatens QM – 18%
- None of the above – 20%
These results are nearly indistinguishable from random choices.
Schrödinger's cat and macroscopic superpositions
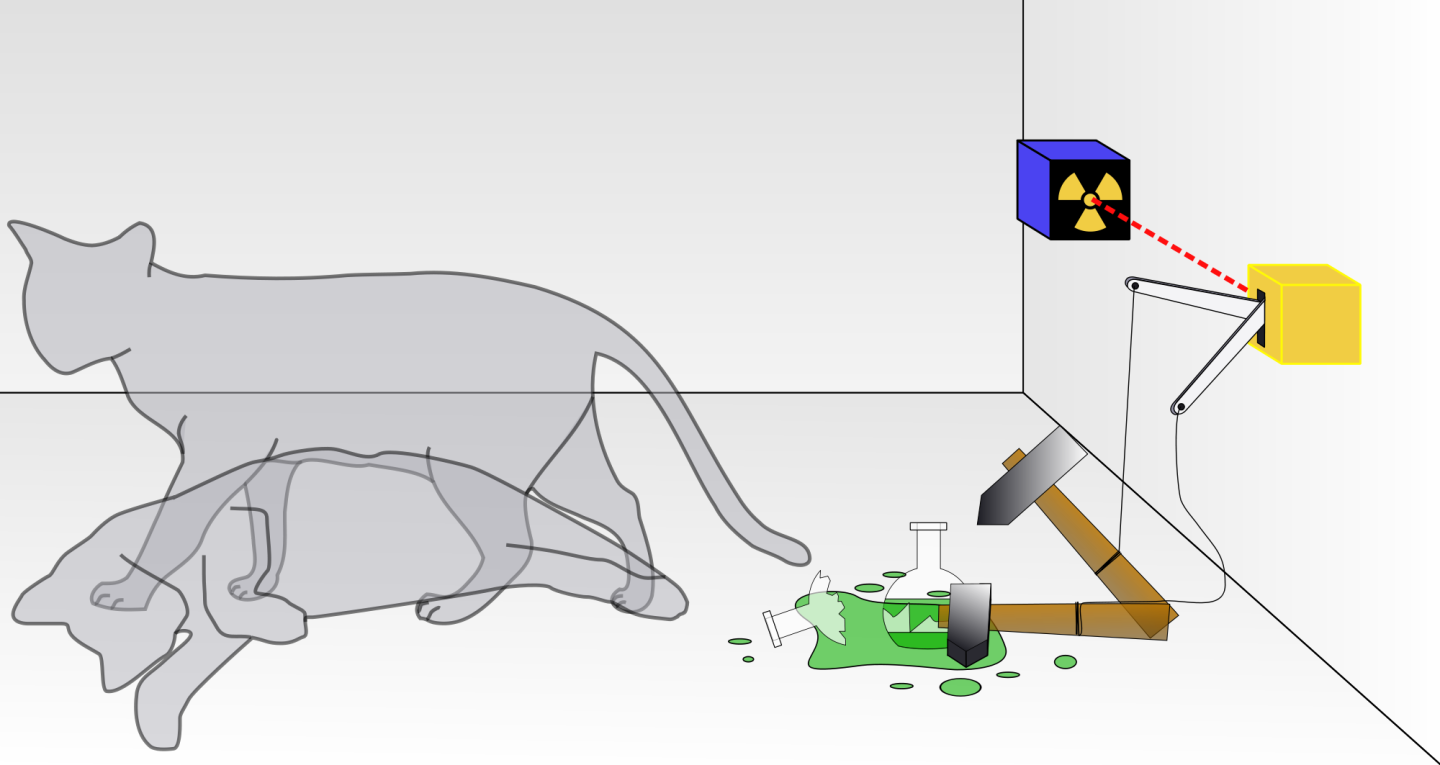
The plight of Schrödinger's Cat is known to many readers. A cat, a conscious, complex quantum system, is placed in a box. Also in the box is a radiation-triggered hammer positioned to smash a glass bottle containing cyanide when radiation is detected. Finally, a very weak radiation source that on average emits one particle per hour is placed in the box, and the box is soundproof, opaque, and sealed. You are sitting outside the box. An hour later, is the cat dead, alive, neither, or both?
The structure of the experiment amplifies an issue accurately described by QM (has a particular radioactive atom decayed?) into what appears to be a classical issue (is the cat alive or dead?). We want to see at what step in the experiment the result stops being quantum mechanical and becomes a definite classical yes or no.
One direction of argument holds that until the box is opened, that cat is in a quantum superposition of dead cat and live cat. On the other hand, if the cat qualifies as an observer, it at least knows if it is alive. (In order for the cat to know it is dead depends on the physical existence of an afterlife – not a standard assumption in QM.) Discussions can become heated, as there are many possible answers.

In the many-worlds theories, the fate of the cat is a bit different. When the box is opened, the universe splits into two – one containing a live cat, the other containing a dead cat.
Schrödinger's Cat led to a specific quantum mechanics question on the QPNR poll: Are superpositions of macroscopically distinct states (such as a dead/alive cat) possible in principle, possible in a laboratory, or impossible in principle?
- Macroscopic superpositions are possible in principle – 55%
This issue is significant, as it can be tested experimentally.
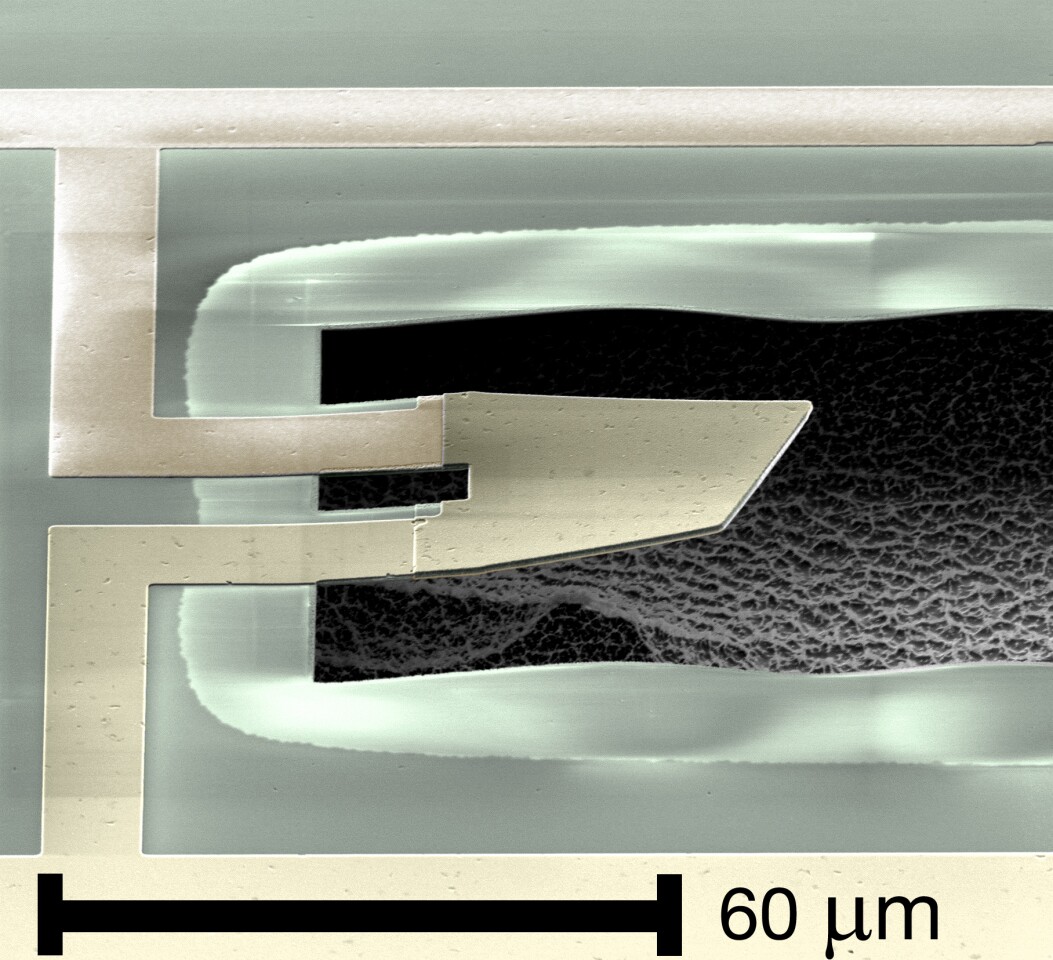
The largest system that has been successfully put into quantum superposition is a quantum microphone weighing about a nanogram (ten trillion atoms) with a volume around 450 cubic microns. This isn't very large, but is far beyond sizes associated with the usual atomic and subatomic interactions which we usually associate with quantum mechanics. The rapid evolution of the field in creating quantum superpositions of larger and larger objects is probably part of the reason that the QPNR poll was rather positive about macroscopic superpositions. This will be a theme – if you can test an idea, consensus forms over time.
Reality or description?
One issue at the foundations of QM involves the physical reality of quantum states. The QPNR poll asked if quantum states only describe reality (are epistemic), or if quantum states are as real as an electric field whose strength can easily be measured (are ontic).
- Epistemic – 27%
- Ontic – 24%
- Both – 33%
- Purely statistical – 3%
- Other – 13%
The answers to this very crucial question are consistent with random responses – the collective confusion appears very large.
Randomness in QM
Another fundamental issue in quantum mechanics involves the randomness of individual quantum events, such as the decay of a radioactive atom. Quantum mechanics predicts behavior that is consistent with random decays having a characteristic half-life for a given decay mode. But is the decay process actually random, or does it just seem that way? The QPNR poll offers four options: Hidden determinism; only appears to be random; irreducible randomness; and randomness is a fundamental concept in nature. Hidden determinism is Einstein's view – there is a hidden clockwork underlying what we perceive as quantum reality. Phenomena are really classical and mechanistic, but we can't see that at present.
The universe only appears to be random in Everett-like many-world interpretations, in which the perception of randomness is an artifact of finding yourself in only one of the new branches of the universe.
The tricky part is deciding on the difference between irreducible randomness and randomness as a fundamental concept in nature. The meaning of the latter is particularly fuzzy. Roughly speaking, irreducible randomness describes a universe in which measured phenomena yield unpredictable results, while fundamental randomness describes a universe whose innermost workings are random. Fundamental randomness is not hidden determinism, saying rather that if there are sublevels of reality, they are also random.
The QPNR answers are:
- Hidden determinism – 0%
- Apparent randomness – 7%
- Irreducible randomness – 40%
- Fundamental randomness – 53%
The lack of support for hidden determinism is probably related to the many experimental tests of Bell's Theorem, which strongly suggest the inapplicability of hidden-variable theories to our universe.
Apparent randomness received fewer than half the votes received by Everett-like interpretations, suggesting that not all Everett supporters agree that the randomness observed therein is apparent.
Irreducible randomness received 40 percent of the votes, while fundamental randomness received 53 percent. It would appear that confusion between these two positions is not limited to your scribe, as all fundamentally random systems are also irreducibly random, but the voting went the other way.
Science or personal prejudice?
To sum up the state of the field of QM interpretations, one particular QPNR poll question is quite revealing. The question is simply: How much is the choice of interpretation a matter of personal philosophical prejudice?
- A lot – 58%
- A little – 27%
- None at all – 15%
Eighty-five percent of those polled believe that the choice of QM interpretation depends to some extent on one's personal philosophical leanings. More than any of the other questions and answers, this shows that the interpretation of quantum mechanics, at present, is not science, little as I like to admit it.
A sign that a description of nature is not fundamental is when it provides little if any justification for working. However, this is also a sign of a new fundamental description of nature lacking the correct language to make clear how and why it works. Personally, I believe the key to answering Feynman's question "But how can it be like that?" is linguistic – we lack a viewpoint and language from which understanding can flow. But the question, entertaining as it is, is really beyond my pay grade.
Sources: arXiv.com, Interpretations of Quantum Mechanics: a critical survey







